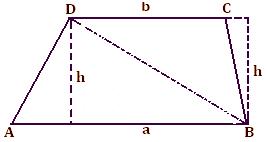
Here we will learn how to use the formula to find the area of trapezium.
Area of trapezium ABCD = Area of ∆ ABD + Area of ∆ CBD
= 1/2 × a × h + 1/2 × b × h
= 1/2 × h × (a + b)
= 1/2 (sum of parallel sides) × (perpendicular distance between them)
Examples
1. The length of the parallel sides of a trapezium are in the rat: 3 : 2 and the distance between them is 10 cm. If the area of trapezium is 325 cm², find the length of the parallel sides.
Solution:
Let the common ration be x,
Then the two parallel sides are 3x, 2x
Distance between them = 10 cm
Area of trapezium = 325 cm²
Area of trapezium = 1/2 (p₁ + p₂) h
325 = 1/2 (3x + 2x) 10
⇒ 325 = 5x × 5
⇒ 325 = 25x
⇒ x = 325/25
Therefore, 3x = 3 × 13 = 39 and 2x = 2 × 13 = 26
Therefore, the length of parallel sides area are 26 cm and 39 cm.
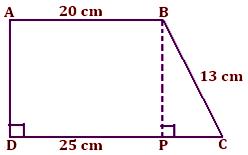
2. ABCD is a trapezium in which AB ∥ CD, AD ⊥ DC, AB = 20 cm, BC = 13 cm and DC = 25 cm. Find the area of the trapezium.
From B draw BP perpendicular DC
Therefore, AB = DP = 20 cm
So, PC = DC – DP
= (25 – 20) cm
= 5 cm
Now, area of trapezium ABCD = Area of rectangle ABPD + Area of △ BPC
△BPC is right angled at ∠BPC
Therefore, using Pythagoras theorem,
BC² = BP² + PC²
13² = BP² + 5²
⇒ 169 = BP² + 25
⇒ 169 – 25 = BP²
⇒ 144 = BP²
⇒ BP = 12
Now, area of trapezium ABCD = Area of rectangle ABPD + Area of ∆BPC
= AB × BP + 1/2 × PC × BP
= 20 × 12 + 1/2 × 5 × 12
= 240 + 30
= 270 cm²
3. The area of a trapezium is 165 cm² and its height is 10 cm. If one of the parallel sides is double of the other, find the two parallel sides.
Solution:
Let one side of trapezium is x, then other side parallel to it = 2x
Area of trapezium = 165 cm²
Height of trapezium = 10 cm
Now, area of trapezium = 1/2 (p₁ + p₂) × h
⇒ 165 = 1/2(x₁ + 2x) × 10
⇒ 165 = 3x × 5
⇒ 165 = 15x
⇒ x = 165/15
⇒ x = 11
Therefore, 2x = 2 × 11 = 22
Therefore, the two parallel sides are of length 11 cm and 22 cm.
4. Find the area of a trapezium whose parallel sides are AB = 12 cm, CD = 36 cm and the non-parallel sides are BC = 15 cm and AG = 15 cm.
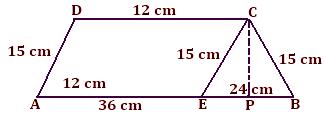Solution:
In trapezium ABCD, draw CE ∥ DA.
Now CE = 15 cm
Since, DC = 12 cm so, AE = 12 cm
Also, EB = AB – AE = 36 – 12 = 24 cm
Now, in ∆ EBC
S = (15 + 15 + 24)/2
= 54/2
= 27
= √(27 × 12 × 12 × 3)
= √(3 × 3 × 3 × 3 × 2 × 2 × 2 × 2 × 3 × 3)
= 3 × 3 × 3 × 2 × 2
= 108 cm²
Draw CP ⊥ EB.
Area of ∆EBC = 1/2 × EB × CP
108 = 1/2 × 24 × CP
108/12 = CP
⇒ CP = 9 cm Therefore, h = 9 cm
Now, area of triangle = √(s(s – a) (s – b) (s – c))
= √(27 (27 – 15) (27 – 15 ) (27 – 24))
Now, area of trapezium = 1/2(p₁ + p₂) × h
= 1/2 × 48 × 9
= 216 cm²