Overview
The whole numbers are part of the number system which includes all the positive integers from 0 to infinity. These numbers exist in the number line. Hence, they are all real numbers. We can say, all the whole numbers are real numbers, but not all the real numbers are whole numbers. Thus, we can define whole numbers as the set of natural numbers and 0. Real numbers are the set of all these types of numbers, i.e., natural numbers, whole numbers, integers, and fractions.
The complete set of natural numbers along with ‘0’ are called whole numbers. The examples are: 0, 11, 25, 36, 999, 1200, etc.
Whole Numbers
The whole numbers are the numbers without fractions and it is a collection of positive integers and zero. It is represented by the symbol “W” and the set of numbers are {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,……………}. Zero as a whole represents nothing or a null value.
|
Symbol
The symbol to represent whole numbers is the alphabet ‘W’ in capital letters.
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}
Thus, the whole numbers list includes 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ….
Facts:
|
Whole numbers include natural numbers that begin from 1 onwards.
Let us look at some examples of whole numbers.
| Whole Numbers | NOT Whole Numbers |
| 0, 14, 97, 345, 8901, and 888888 | -5 (Negative numbers), 7.3 (Decimals), ⅘ (Fractions) |
Whole Numbers on Number Line
The set of whole numbers can be displayed on the number line as shown below.
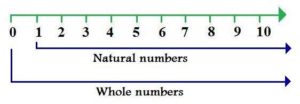
Difference between Whole Numbers and Natural numbers
| Whole Numbers | Natural Numbers |
| Whole numbers include all natural numbers and zero. | Natural numbers are generally used for counting objects or things. |
| The set of whole numbers is, W = {0,1,2,3,…}. | The set of natural numbers is, N = {1,2,3,…}. |
| The smallest whole number is 0. | The smallest natural number is 1. |
From these differences, we can easily deduce that every whole number other than 0 is a natural number. We can say that the set of natural numbers is a subset of whole numbers.
Properties of Whole Numbers
The basic operation of addition, subtraction, multiplication, and division give rise to four main properties of whole numbers.
-
Additive Identity
When a whole number is added to 0, its value remains unchanged, i.e., if x is a whole number then x + 0 = 0 + x = x
Example:
Consider two whole numbers 0 and 11.
0 + 11 = 11
11 + 0 = 11
Here, 0 + 11 = 11 + 0 = 11
Therefore, 0 is called the additive identity of whole numbers.
-
Multiplicative Identity
When a whole number is multiplied by 1, its value remains unchanged, i.e., if x is a whole number then x . 1 = x = 1 . x
Example:
Consider two whole numbers 1 and 15.
1 × 15 = 15
15 × 1 = 15
Here, 1 × 15 = 15 = 15 × 1
Therefore, 1 is the multiplicative identity of whole numbers.
-
Multiplication by zero
When a whole number is multiplied to 0, the result is always 0, i.e., x.0 = 0.x = 0
Example:
0 × 12 = 0
12 × 0 = 0
Here, 0 × 12 = 12 × 0 = 0
Thus, for any whole number multiplied by 0, the result is always 0.
-
Division by zero
The division of a whole number by o is not defined, i.e., if x is a whole number then x/0 is not defined.
