Addition of Integers
Addition of integers having the same sign
1. The sum of two positive integers is the sum of their absolute values with a positive sign.
Example:
Add (+ 6) + (+4).
Solution: On a number line, first draw an arrow from 0 to 6 and then go 4 steps ahead. The tip of the last arrow reaches +10. So, (+ 6) + (+ 4) = +10
2. The sum of two negative integers is the sum of their absolute values with negative sign(-).
Example:
Add (-3) + (-4).
Solution: On a number line, first we draw an arrow on the left side of zero from 0 to -3 and then further move to the left 4 steps. The tip of the last arrow is at -7. So, (-3) + (-4) = (-7)
Addition of integers having opposite signs
The sum of two integers having opposite signs is the difference of their absolute values with the sign of integer of greater absolute value.
Example:
Add(+6) + (-9).
Solution: On a number line, first we draw an arrow from 0 to 6 on the right and then go 9 steps to the left. The tip of the last arrow is at -3. So, (+6) + (-9) = (-3)
Subtraction of Integers
In subtraction, we change the sign of the integer which is to be subtracted and then add it to the first integer. In other words, if a and b are two integers, then a – b = a + (-b)
Example:
Subtract 5 from 12.
Solution: (12) – (5) = (12) + (-5) = 7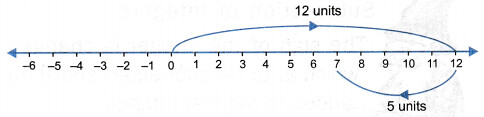
Example:
Subtract -7 from -15.
Solution: (-15) – (-7) = (-15) + (7)= -8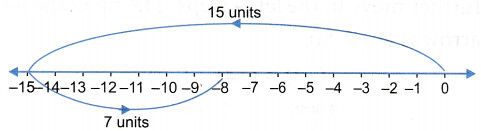
Example:
Subtract (-5) from 4.
Solution: 4 – (-5) = 4 + (5) = 9
To subtract (-5) from 4, we have to find a number which when added to (-5) gives us 4. So, on the number line we start from (-5) and move up to 4. Now find how many units we have moved. We have moved 9 units.
So, 4-(-5) = 9
Multiplication of Integers
Multiplication of integers having the same sign
When two integers have the same sign, their product is the product of their absolute values with positive sign.
Examples
(a) (+6) × (+7) = + 42 or 42
(b) (+5) × (+10) = + 50 or 50
(c) (-20) × (-6) = 120
Multiplication of integers having opposite signs
The product of two integers having opposite signs is the product of their absolute values with negative sign.
Examples
(a) (-10) × (8) = (- 80)
(b) (- 5) × (7) = (-35)
(c) (12) × (-3) = (-36)
Division of Integers
Division of integers having the same sign
The division of two integers having the same sign is the division of their absolute value with a positive sign. If both integers have the same sign, then the quotient will be positive.
Examples:
(a) (+9) ÷ (+3) = (3)
(b) (-9) ÷ (-3) = (3)
(c) (-24) ÷ (-12) = (2)
Division of integers having opposite signs
If both integers have different signs, the quotient will be negative.
Examples:
(a) 12 ÷ (-3) = (-4)
(b) (-10) ÷ (5) = (-2)
(c) (-18) ÷ (3) = (-6)
Example:
Evaluate (-13) – (-7 – 6).
Solution:
(-13) – (-7 – 6)
= (-13) -(-13)
= (-13) + (13) (Opposite to each other) = 0
Example:
Subtract (-5128) from 0.
Solution:
0 – (-5128) = 0 + 5128 = 5128
Remember!
Addition of integers
(a) The sum of two integers with like signs is the sum of their absolute values with the same sign.
(b) The sum of two integers with unlike signs is the difference of their absolute values with _the sign of the greater absolute value.
Subtraction of integers
The sign of the integer is changed which is to be subtracted and then added to the first integer.
Multiplication of integers
(a) When two integers have the same sign, their product is the product of their absolute values with a positive sign.
(b) The product of two integers having opposite signs is the product of their absolute values with a negative sign.
Division of integers
(a) If integers have the same sign, the quotient is always positive.
(b) If integers have opposite signs, the quotient will be negative.
Sign Rules:
