Corresponding Parts of Congruent Triangles
As we know that the corresponding parts of congruent triangles are equal. While dealing with the concepts related to triangles and solving questions, we often make use of the abbreviation cpct in short words instead of full form.
Rules
After proving triangles congruent, the remaining dimension can be predicted without actually measuring the sides and angles of a triangle. Different rules of congruency are as follows.
- SSS (Side-Side-Side)
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- AAS (Angle-Angle-Side)
- RHS (Right angle-Hypotenuse-Side)

SSS (Side-Side-Side)
If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule.

In the above-given figure, AB= PQ, BC = QR and AC=PR, hence Δ ABC ≅ Δ PQR.
SAS (Side-Angle-Side)
If any two sides and the angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle, then the two triangles are said to be congruent by SAS rule.
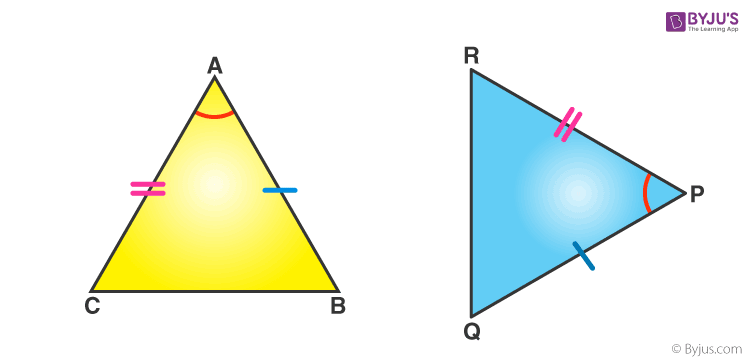
In above given figure, sides AB= PQ, AC=PR and angle between AC and AB equal to angle between PR and PQ i.e. ∠A = ∠P. Hence, Δ ABC ≅ Δ PQR.
ASA (Angle-Side- Angle)
If any two angles and the side included between the angles of one triangle are equivalent to the corresponding two angles and side included between the angles of the second triangle, then the two triangles are said to be congruent by ASA rule.

In above given figure, ∠ B = ∠ Q, ∠ C = ∠ R and sides between ∠B and ∠C , ∠Q and ∠ R are equal to each other i.e. BC= QR. Hence, Δ ABC ≅ Δ PQR.
AAS (Angle-Angle-Side) [Application of ASA]
AAS stands for Angle-Angle-Side. When two angles and a non-included side of a triangle are equal to the corresponding angles and sides of another triangle, then the triangles are said to be congruent.
AAS congruence can be proved in easy steps.
Suppose we have two triangles ABC and DEF, where,

∠B = ∠E [Corresponding angles] ∠C = ∠F [Corresponding angles] And
AC = DF [Adjacent sides]
By angle sum property of triangle, we know that;
∠A + ∠B + ∠C = 180 ………(1)
∠D + ∠E + ∠F = 180 ……….(2)
From equation 1 and 2 we can say;
∠A + ∠B + ∠C = ∠D + ∠E + ∠F
∠A + ∠E + ∠F = ∠D + ∠E + ∠F [Since, ∠B = ∠E and ∠C = ∠F] ∠A = ∠D
Hence, in triangle ABC and DEF,
∠A = ∠D
AC = DF
∠C = ∠F
Hence, by ASA congruency,
Δ ABC ≅ Δ DEF
RHS (Right angle- Hypotenuse-Side)
If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule.

In above figure, hypotenuse XZ = RT and side YZ=ST, hence ∆ XYZ ≅ ∆ RST.