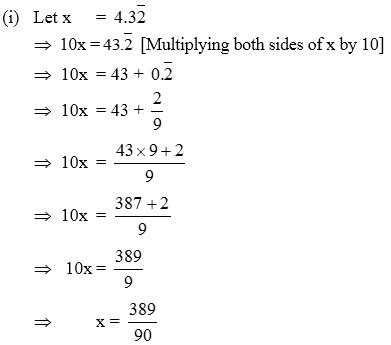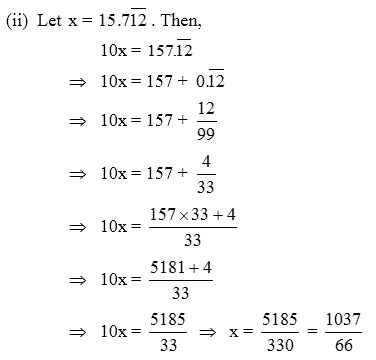Decimals
A decimal is a number that consists of a whole and a fractional part. Decimal numbers lie between integers and represent numerical value for quantities that are whole plus some part of a whole.
For example, in the given image, we have one whole pizza and a half of another pizza. This can be represented in two ways:

Fractional Form: In fraction form, we can write that there is one and one-half of a pizza. That is 1 1/2 pizza.
Decimal Form: In decimal form, we will write this as 1.5 pizzas. Here, the dot represents the decimal point and the number before the dot, i.e., “1” represents one whole pizza and the number behind the decimal point represents the half pizza or the fractional part.
You might have seen decimal numbers like these when you go grocery shopping or on a weighing machine or even a game of baseball!
What is a Decimal?
We get decimals when we break a whole into smaller parts. A decimal number then has two components: a whole number part and a fractional part. The decimal place value system for the whole part of a decimal number is the same as the whole number value system. However, we get the fractional part of the decimal number as we move toward the right after the decimal point. The given image shows the decimal place value chart:

Note that as we go from left to right in the decimal place value system, each values is 110 times smaller than the value to its left.
The first place after the decimal point is called the “tenths”, which represents a place value of 1/10 of the whole or one-tenth of the whole. In decimal form, this fraction is written as “0.1”.
Such fractions whose denominator is 10 or a positive power of 10 is called a decimal fraction.
The second place is called the “hundredths”, which represents a place value of 1/100 of the whole or one-hundredth of the whole. In numerical form, this decimal fraction is written as “0.01”.
And the third place is called the “thousandths”, which represents a place value of 1/1000 of the whole or one-thousandth of the whole. In numerical form, this decimal fraction is written as “0.001”.
For example, 34.5 is a decimal number.
Here, 34 is a whole number part and 5 is the fractional part.
“.” is the decimal point.
Let us discuss some other examples.
Here is the number “thirty-four and seven-tenths” written as a decimal number:

The decimal point goes between Ones and Tenths
34.7 has 3 Tens, 4 Ones and 7 Tenths
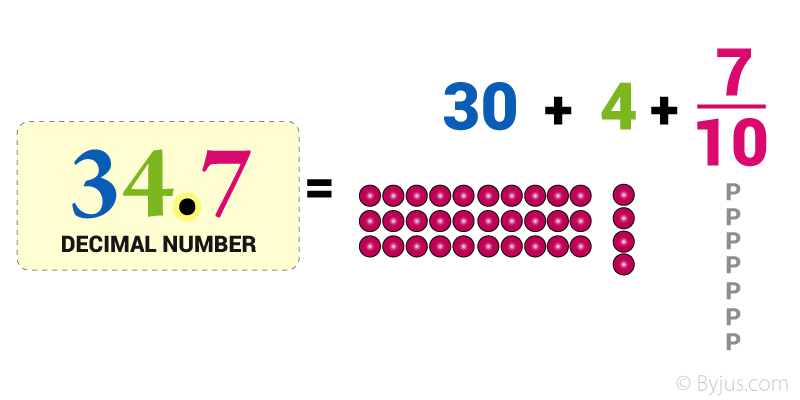
How to Read a Decimal
An informal way to read a decimal is by reading the whole part of the decimal number as you would read any whole number and then reading the decimal dot as “point” and then reading each digit of the rational part individually.
For example, the number 17.48 would be read as “Seventeen point four eight”.
However, a more formal way to read decimals is to read the whole part as a whole number, then the decimal dot as “and” and then reading the fractional part altogether but using the place value of the last digit with it.
For example, take a look at the given number
25.678
Here, the whole part is 25 and the place value of the last digit, 8, is thousandths. So we will read this number as “Twenty-five and six hundred seventy-eight thousandths”.
Types of Decimals
Based on the number of digits after the decimal point, the decimal numbers can be divided into two categories:
- Like decimals: Two decimal numbers are said to be “like” decimals if they have the same number of digits after the decimal point. For example, 6.34 and 2.67 both have two digits after the decimal point so they are Like decimals.
- Unlike decimals: Two decimal numbers are said to be “unlike” decimals if they have different number of digits after the decimal point. For example, 5.3 and 6.873 both have different number of digits after the decimal point so they are unlike decimals.
Conversion Of Decimal Numbers Into Rational Numbers Of The Form m/n
Case I: When the decimal number is of a terminating nature.
- Step-1: Obtain the rational number.
- Step-2: Determine the number of digits in its decimal part.
- Step-3: Remove decimal point from the numerator. Write 1 in the denominator and put as many zeros on the right side of 1 as the number of digits in the decimal part of the given rational number.
- Step-4: Find a common divisor of the numerator and denominator and express the rational number to lowest terms by dividing its numerator and denominator by the common divisor.
Case II: When decimal representation is of non-terminating repeating nature.
In a non terminating repeating decimal, there are two types of decimal representations
- A decimal in which all the digit after the decimal point are repeated. These type of decimals are known as pure recurring decimals.
![]()
- A decimal in which at least one of the digits after the decimal point is not repeated and then some digit or digits are repeated. This type of decimals is known as mixed recurring decimals.
![]()
Conversion Of A Pure Recurring Decimal To The Form p/q
- Step-1: Obtain the repeating decimal and put it equal to x (say)
- Step-2: Write the number in decimal form by removing bar from the top of repeating digits and listing repeating digits at least twice. For sample,

- Step-3: Determine the number of digits having bar on their heads.
- Step-4: If the repeating decimal has 1 place repetition, multiply by 10; a two-place repetition, multiply by 100; a three-place repetition, multiply by 1000, and so on.
- Step-5: Subtract the number in step 2 from the number obtained in step 4
- Step-6: Divide both sides of the equation by the coefficient of x.
- Step-7: Write the rational number in its simplest form.
Conversion Of A Mixed Recurring Decimal To The Form p/q
- Step-1: Obtain the mixed recurring decimal and write it equal to x (say)
- Step-2: Determine the number of digits after the decimal point which does not have a bar on them. Let there be n digits without a bar just after the decimal point
- Step-3: Multiply both sides of x by 10n so that only the repeating decimal is on the right side of the decimal point.
- Step-4: Use the method of converting pure recurring decimal to the form p/q and obtain the value of x
Examples
1. Express each of the following numbers in the form p/q.
(i) 0.15 (ii) 0.675 (iii) –25.6875
Solution:

2. Express each of the following decimals in the form p/q.
![]()
Solution:

The above example suggests us the following rule to convert a pure recurring decimal into a rational number in the form p/q.
3. Express the following decimals in the form.
![]()
Solution:


4. Express each of the following mixed recurring decimals in the form p/q
![]()
Solution: