Direct Proportion

Direct proportion is a mathematical comparison between two numbers where the ratio of the two numbers is equal to a constant value. The proportion definition says that when two ratios are equivalent, they are in proportion. The symbol used to relate the proportions is “∝”.

“When the relationship between two quantities is such that if we increase one, the other will also increase, and if we decrease one the other quantity will also decrease, then the two quantities are said to be in a direct proportion”.

For example, if there are two quantities x and y where x = number of candies and y = total money spent. If we buy more candies, we will have to pay more money, and we buy fewer candies then we will be paying less money. So, here we can say that x and y are directly proportional to each other. It is represented as x ∝ y. Direct proportion is also known as direct variation.

Some real-life examples of direct proportionality are given below:

• The number of food items is directly proportional to the total money spent.
• Work done is directly proportional to the number of workers.
• Speed is in direct proportion to the distance w.r.t a fixed time.

In our day-to-day life, we observe that the variations in the values of various quantities depending upon the variation in values of some other quantities.

For example: if the number of individuals visiting a restaurant increases, earning of the restaurant also increases and vice versa. If more number of people are employed for the same job, the time taken to accomplish the job decreases.

Sometimes, we observe that the variation in the value of one quantity is similar to the variation in the value of another quantity that is when the value of one quantity increases then the value of other quantity also increases in the same proportion and vice versa. In such situations, two quantities are termed to exist in direct proportion.

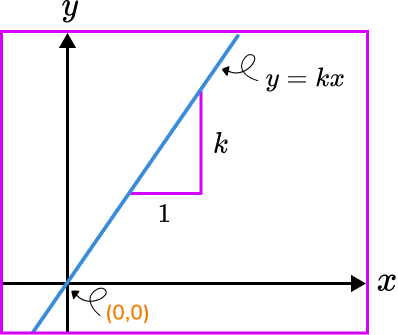
Direct Proportion Symbol and Constant of Proportionality

The symbol for “direct proportional” is ‘∝’  (One should not confuse with the symbol for infinity ∞). Two quantities existing in direct proportion can be expressed as;

x ∝ y

x/y = k

x = ky

k is a non-zero constant of proportionality.

Where x and y are the value of two quantities and k are a constant known as the constant of proportionality. If x₁, y₁ is the initial values and x₂, y₂ are the final values of quantities existing in direct proportion. They can be expressed as,

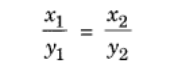
Example:
A recipe for 6 cupcakes needs 1 cup of flour. The number of cupcakes you can make varies directly with the amount of flour, which means for making more cup cakes we require more flour. How many cupcakes can you make with 4 cups of flour? 

Solution:

Let $x$ = amount of flour and $y$ = number of cupcakes 

Since $y\alpha x$, 

$y=kx$     . . . ($1$) 

For $6$ cup cakes we require $1$ cup of flour. 

$\therefore$ for $x=6$, $y=1$

put the above values in equation ($1$) 

$6=k\times 1$ 

$6=k$ 

$\therefore k=6$ 

$\therefore y=6x$   . . . ($2$) 

Now we have to find the number cup cakes that can be made in four cups of flour.

When $x=\mathrm{4,}$ $y=?$

Using equation ($2$)

$y=6x=6\times 4$

$\therefore y=24$

So you can make $24$ cupcakes in $4$ cups of flour.

Example:

An electric pole, 7 meters high, casts a shadow of 5 meters. Find the height of a tree that casts a shadow of 10 meters under similar conditions.

Solution:

Let the height of the tree be x meters. We know that if the height of the pole increases the length of shadow will also increase in same proportion. Hence, we observe that the height of the tree and the length of its shadow exist in direct proportion. In other words height of pole is directly proportional to the length of its shadow. Thus,

A train travels 200 km in 5 hours. How much time it will take to cover 600 km?

Solution:

Let the time taken be T hours.

We know that time taken is directly proportional to distance covered.

Hence,

x1 / y1 = x2 / y2

⇒ 200 / 5 = 600 / T

T = 15 hours.