Math Lab Activity

– Exploring Decimal Squares

Objective:

In this activity, you will use Decimal Squares to compare, add, subtract, and multiply decimal numbers. Each Decimal Square represents different decimal values, helping you visualize and solve problems involving decimals.

Materials Needed:

• Decimal Squares (paper or visual aids)
• Colored writing utensils
• The overhead projection system (if available)

Instructions:

1. Understanding Decimal Squares:
   Start by learning about Decimal Squares. These squares have an area of 100 square units, with each small square representing 0.01 (one hundredth). Each column (10 squares) represents 0.1 (one-tenth) of the whole square.
2. Representing Decimals:
   Shade 0.2 (two columns of 10 square units) on a Decimal Square. Explain that this represents two-tenths of the whole square. Next, shade 0.32 (three columns and 2 square units) on a Decimal Square to show thirty-two hundredths.
3. Exploring Operations:
   Use Decimal Squares and colored writing utensils to shade areas that represent problems involving decimals. Discuss and demonstrate how to find solutions to these problems using the shaded squares. Make sure each Decimal Square has the problem and solution displayed below it.
4. Examples and Demonstrations:
   Use the provided examples as demonstrations to guide your understanding. Ensure that the problems you design do not involve the thousandth place, as these might not be solvable using Decimal Squares.
5. Problem Solving:
   As you work through various problems, consider comparison, addition, subtraction, and multiplication of decimal numbers. Use the shaded areas to visually represent the problems, and use the squares to arrive at your solutions.
6. Reflection:
   After solving a set of problems, gather the strategies you used and the insights you gained from using Decimal Squares. Reflect on how these visual aids helped you better understand decimal operations.

Through this activity, you’ll enhance your grasp of decimals and gain a practical way to visualize and solve problems involving decimal values.

Example:

The following problems can be used to explain the use of Decimal Squares to students.

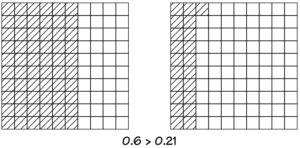
1. Shade 0.6 in the first Decimal Square (starting on the left) and 0.21 in the second (starting on the left). Then compare the shaded areas to discover the answer to the problem, ‘‘To solve 0.6 0.21, fill in the blank with >, <, =.’’

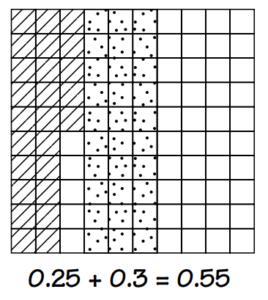
2. Shade 0.25 using one color and 0.3 using another color. Add up the entire area to discover the sum of 0.25 and 0.3.

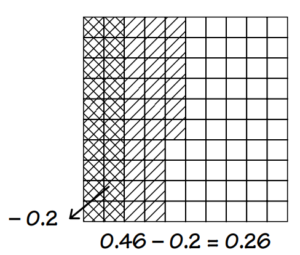
3. Shade 0.46 in one color, then shade 0.2 in the area already shaded using another color. The part of the figure shaded twice will be subtracted from the total area. Ask students what decimal represents the area remaining.

4. Shade 0.5 vertically and 0.4 horizontally. The number of squares in the rectangular area of overlap represents the solution to the problem 0.5 × 0.4.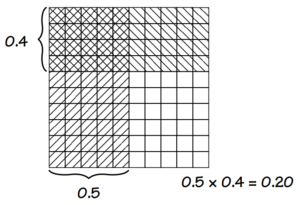

Ignite Your Mathematical Mind:

Try the following problems using Decimal Squares. 

1. Insert <, >, or = to make the statement 0.34 0.3 true.

2. Insert <, >, or = to make the statement 0.5 0.50 true.

3. Find 0.4 + 0.27.

4. Find 0.72 + 0.15.

5. Find 0.54 − 0.3.

6. Find 0.68 − 0.4.

7. Find 0.5 × 0.6.

8. Find 0.3 − 0.8.

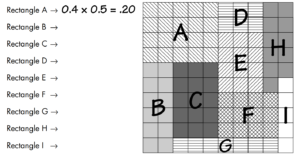
9. Using the Decimal Square below, state the decimal multiplication problem represented by the rectangle shaded.