Course Content
Chapter 01 – Operations on Sets
The set operations are performed on two or more sets to obtain a combination of elements as per the operation performed on them. In a set theory, there are three major types of operations performed on sets, such as: Union of sets (∪) The intersection of sets (∩) Difference of sets ( – ) In this lesson we will discuss these operations along with their Venn diagram and will learn to verify the following laws: Commutative, Associative, Distributive, and De-Morgans' law.
0/13
Subsets and Super Sets
03:10
Venn Diagrams
03:32
Operations on Set
00:00
Union of Sets
16:15
Intersection of Sets
17:12
Difference of Sets
13:13
Complement of Sets
19:42
Venn Diagrams (Three or More Sets)
03:22
Commutative Law of Union and Intersection
02:53
Associative Law of Union and Intersection
05:01
Distributive Law over Union and Intersection
04:13
De Morgan’s Law
00:00
Date To Math - Quiz
Chapter 02 – Real Numbers
All real numbers follow three main rules: they can be measured, valued, and manipulated. Learn about various types of real numbers, like whole numbers, rational numbers, and irrational numbers, and explore their properties. In this chapter, we will learn about Squares and cubes of real numbers and find their roots.
0/5
Irrational Numbers
03:14
Squares
03:04
Square Roots
03:49
Cubes and Cube Roots
00:00
Dare To Math - Quiz
Chapter 03 – Number System
The number system or the numeral system is the system of naming or representing numbers. There are different types of number systems in Mathematics like decimal number system, binary number system, octal number system, and hexadecimal number system. In this chapter, we will learn different types and conversion procedures with many number systems.
0/13
Number System
08:13
Conversion – Base 2
00:00
Addition in Binary System
03:02
Subtraction in Binary System
02:32
Multiplication in Binary System
02:43
Conversion – Base 5
00:00
Addition in Base 5
01:55
Subtraction in Base 5
01:38
Multiplication in Base 5
04:17
Conversion – Base 8
08:19
Addition & Subtraction in Base 8
06:07
Multiplication in Base 8
04:39
Dare To Math - Quiz
Chapter 04 – Financial Arithmetic
Financial mathematics describes the application of mathematics and mathematical modeling to solve financial problems. In this chapter, we will learn about partnership, banking, conversion of currencies, profit/markup, percentage, and income tax.
0/10
Compound Proportion
05:10
Partnership
07:18
Inheritance
09:54
Conversion of Currencies
03:13
Profit or Markup
07:01
Percentage
08:31
Taxes
03:46
Income Tax
02:16
Banking
06:17
Dare To Math - Quiz
Chapter 05 – Polynomials
In algebra, a polynomial equation contains coefficients, exponents, and variables. Learn about forming polynomial equations. In this chapter, we will study the definition and the three restrictions of polynomials, we'll tackle polynomial equations and learn to perform operations on polynomials, and learn to avoid common mistakes.
0/6
Algebraic Expression
00:00
Polynomials
00:00
Addition and Subtraction of Polynomial
00:00
Multiplication of Polynomials
02:43
Division of Polynomial
00:00
Dare To Math - Quiz
Chapter 06 – Factorization, Simultaneous Equations
In algebra, factoring is a technique to simplify an expression by reversing the multiplication process. Simultaneous Equations are a set of two or more algebraic equations that share variables and are solved simultaneously. In this chapter, we will learn about factoring by grouping, review the three steps, explore splitting the middle term, and work examples to practice verification and what simultaneous equations are with examples. Find out how to solve the equations using the methods of elimination, graphing, and substitution.
0/10
Algebraic Formulas
06:35
Stimulation – Area Model Algebra
00:00
Factorization
00:00
Manipulation of Algebraic Expression
00:00
Stimulation – Equality Explorer
00:00
Linear Equations in One Variable
00:00
Simultaneous Linear Equations
00:00
Stimulation – Equality Explorer (Two Variables)
00:00
Elimination
00:00
Let's Try
Chapter 07 – Fundamentals of Geometry
Geometry is the study of different types of shapes, figures, and sizes. It is important to know and understand some basic concepts. We will learn about some of the most fundamental concepts in geometry, including lines, polygons, and circles.
0/4
Parallel Lines
05:36
Polygons
00:00
Circles
00:00
Dare To Math - Quiz
Chapter 08 – Practical Geometry
Geometric construction offers the ability to create accurate drawings and models without the use of numbers. In this chapter, we will discover the methods and tools that will aid in solving math problems as well as constructing quadrilaterals and right-angled triangles.
0/3
Construction of Quadrilaterals
11:16
Construction of a Right Angled Triangle
00:00
Dare To Math - Quiz
Chapter 09 – Areas and Volumes
The volume and surface area of a sphere can be calculated when the sphere's radius is given. In this chapter, we will learn about the shape sphere and its radius, and understand how to calculate the volume and surface area of a sphere through some practice problems. Also, we will learn to use and apply Pythagoras' theorem and Herons' formula.
0/5
Pythagoras Theorem
00:00
Heron’s Formula
00:00
Surface Area, and Volume of a Sphere
00:00
Dare To Math - Quiz
Math Lab
Chapter 10 – Demonstrative Geometry
Demonstrative geometry is a branch of mathematics that is used to demonstrate the truth of mathematical statements concerning geometric figures. In this chapter, we will learn about theorems on geometry that are proved through logical reasoning.
0/5
Reasoning
03:34
Axioms
00:00
Postulate
05:01
Theorems
00:00
Dare To Math - Quiz
Chapter 11 – Trigonometry
Sine and cosine are basic trigonometric functions used to solve the angles and sides of triangles. In this chapter, we will review trigonometry concepts and learn about the mnemonic used for sine, cosine, and tangent functions.
0/6
What is Trigonometry?
00:00
Visualization of Trigonometric Ratios
02:55
Trigonometric Ratios of Complementary Angles
05:21
Simulation – Trig Tour
00:00
Angle of Elevation and Angle of Depression
04:22
Dare To Math - Quiz
Chapter 12 – Information Handling
Frequency distribution, in statistics, is a graph or data set organized to show the frequency of occurrence of each possible outcome of a repeatable event observed many times. Measures of central tendency describe how data sets are clustered in a central value. In this chapter, we will learn to construct the frequency distribution table, and learn more about three measures of central tendency, its importance, and various examples.
0/7
Frequency Distribition
01:03
Bar Graph
07:49
Histogram
00:00
Pie Chart
04:29
Measures of Central Tendency
00:00
Mean, Median, and Mode
00:00
Dare To Math - Quiz
Grade 8 – Mathematics
About Lesson

Compound Proportion

“The proportion involving two or more quantities is called Compound Proportion.”  The quantities could be directly related or inversely related or both.

Rules for Solving Compound Proportions

1. Identify the magnitudes.
2. Order the magnitudes and their data, placing the unknown at the end.
3. Check if is direct or inverse proportionality. (Identify the proportionality relationship between 
    the magnitude to the unknown datum and the others).
4. Transform the data into a proportional fraction. In inverse proportions, operate with inverse 
   fractions.
5. Calculate the value of x.

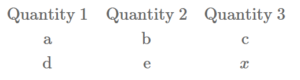
CASE-1
If quantity 1 and quantity 2 are directly related and quantity 2 and quantity 3 are also directly related, then we use the following rule:

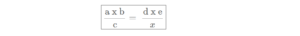
CASE-2
If quantity 1 and quantity 2 are directly related and quantity 2 and quantity 3 are inversely related, then we use the following rule:

CASE-3
If quantity 1 and quantity 2 are inversely related and quantity 2 and quantity 3 are directly related, then we use the following rule:

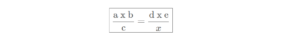
CASE-4
If quantity 1 and quantity 2 are inversely related and quantity 2 and quantity 3 are also inversely related, then we use the following rule:

Example:
195 men working 10 hours a day can finish a job in 20 days. How many men are employed to finish the job in 15 days if they work 13 hours a day?

Solution:
Let x be the no. of men required

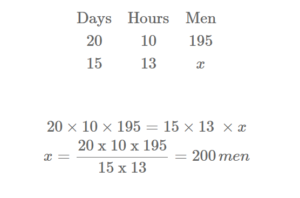
Example:
A soap factory makes 600 units in 9 days with the help of 20 machines. How many units can be made in 12 days with the help of 18 machines?

Solution:

There are two methods to calculate compound proportionality problems: the unitary method or compound 
rule of three.
  • Rule of three.
  • The unitary method.

Rule of three:

Previous
Next
0% Complete