Triangle

A triangle is a three-sided closed shape. A triangle is a three-sided closed polygon. There are different triangles based on the sides and angles of the triangle, such as equilateral, isosceles, acute-angled, obtuse-angled and right-angled triangles etc.

What is a Right Triangle?

A right-angled triangle has three sides, referred to as the ‘base,’ ‘height,’ and ‘hypotenuse.’ One of the angles in a right-angled triangle is 90 degrees, while the other two are sharp. 

A right-angled triangle is a triangle which has one of its three angles equal to 90 degrees. The other two angles are acute angles. The side opposite the right angle is the longest side and is called the hypotenuse. The side which makes the right angle with the base is called perpendicular. Construction of a right-angled triangle is possible when the Hypotenuse and one side from the remaining two sides are known to us.

The requirements for the construction are a ruler and a compass.

Properties of Right Triangle

The properties of the right-angled triangles are listed below:

1. One of the angles in the right triangle is 90 degrees.
2. The longest or largest side of the right triangle is called the hypotenuse.
3. The hypotenuse lies opposite to the right angle.
4. The sum of the other two angles equals the right angle is 90 degrees.
5. The perpendicular drawn from the right angle to the hypotenuse divides the two triangles into similar triangles.
6. The other two angles in a right-angled isosceles triangle are equal, and each being 45 degrees.
7. The sum of interior angles of a right-angled triangle is equal to 180 degrees.

A triangle in which one of the angles is equal to 90° is a right-angled triangle. The side which is directly opposite to the right angle is called the hypotenuse of the longest side. To construct a right-angled triangle, we require the measurements of two of its sides. A compass and a ruler are necessary to construct a right-angled triangle. Now let us see how a triangle PQR with the hypotenuse 7 units and one of its sides to be 6 units.

Construct a triangle PQR, where Angle QPR = 90 degree, PQ = 6 cm and RQ = 7cm

Step of construction of Right Angled Triangle, whose length of hypotenuse and one side are given:

Step 1: Use ruler and draw a line segment PQ of 6cm (as shown below):

Step 2: Use protractor and draw angle of 90 degree at point P (as shown below):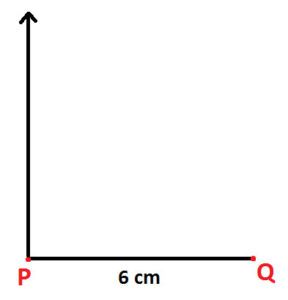

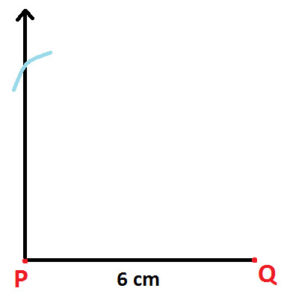
Step 3: Use compass and 7 cm wide open. With Q as center, draw and arc with cut arm of 90 degree angle drawn in step 2 (as shown below)

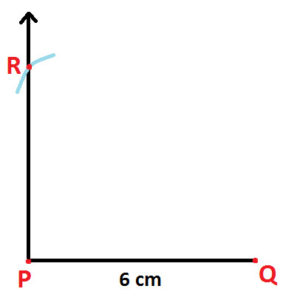
Step 4: Mark point of intersection as point R (as shown below):

Step 5: Join points R and Q (as shown below)

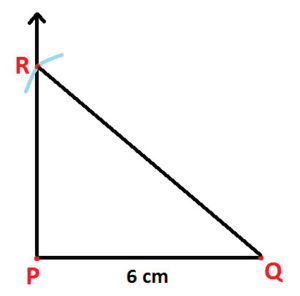
Step 6: Use the rule and check the length of RQ and it has to be of length 7cm. And we get the resultant Right Angled Triangle PQR (as shown below)