Linear Equations

A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form Ax + B = 0. Here, x is a variable, A is a coefficient and B is constant.

The standard form of a linear equation in two variables is of the form

Ax + By = C

Here, x and y are variables, A and B are coefficients and C is a constant.

The linear equations in one variable is an equation which is expressed in the form of ax + b = 0, where a and b are two integers, and x is a variable and has only one solution. For example, 2x+3=8 is a linear equation having a single variable in it. Therefore, this equation has only one solution, which is x = 5/2. 

Linear Equation in One Variable

A linear equation in one variable is an equation which has a maximum of one variable of order 1. It is of the form ax + b = 0, where x is the variable.

This equation has only one solution. A few examples are:

• 3x = 1
• 22x-1=0
• 4x+9=-11

Solving Linear Equations in One Variable

For solving an equation having only one variable, the following steps are followed

• Step 1: Using LCM, clear the fractions if any.
• Step 2: Simplify both sides of the equation.
• Step 3: Isolate the variable.
• Step 4: Verify your answer.

Example of Solution of Linear Equation in One Variable

Let us understand the concept with the help of an example.

For solving equations with variables on both sides, the following steps are followed:

Consider the equation: 5x – 9 = -3x + 19

Step 1: Transpose all the variables on one side of the equation. By transpose, we mean to shift the variables from one side of the equation to the other side of the equation. In the method of transposition, the operation on the operand gets reversed.

In the equation 5x – 9 = -3x + 19, we transpose -3x from the right-hand side to the left-hand side of the equality, the operation gets reversed upon transposition and the equation becomes:

5x – 9 +3x = 19

⇒ 8x -9 = 19

Step 2: Similarly transpose all the constant terms on the other side of the equation as below:

8x -9 = 19

⇒ 8x = 19 + 9

⇒ 8x = 28

Step 3: Divide the equation with 8 on both sides of the equality.

8x/8 = 28/8

⇒ x = 28/8

If we substitute x = 28/8 in the equation 5x – 9 = -3x + 19, we will get 9 = 9, thereby satisfying the equality and giving us the required solution.

How to Solve Linear Equations?

An equation is like a weighing balance with equal weights on both sides. If we add or subtract the same number from both sides of an equation, it still holds true. Similarly, if we multiply or divide the same number on both sides of an equation, it is correct. We bring the variables to one side of the equation and the constant to the other side and then find the value of the unknown variable. This is the way to solve a linear equation with one variable. Let us understand this with the help of an example.

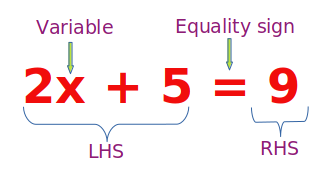
Example: Solve the equation, 2x + 5 = 9.

We perform mathematical operations on the Left-hand side (LHS) and the right-hand side (RHS) so that the balance is not disturbed. So, let us subtract 5 on both sides to reduce the LHS to 2x. This will not disturb the balance. The new LHS is 2x + 5 – 5 = 2x and the new RHS is 9 – 5 = 4. Now, let us divide both sides by 2 to reduce the LHS to x. Thus, we have x = 2. This is one of the ways of solving linear equations in one variable.

Tips on Linear Equations:

• The value of the variable that makes a linear equation true is called the solution or root of the linear equation.
• The solution of a linear equation is unaffected if the same number is added, subtracted, multiplied, or divided into both sides of the equation.
• The graph of a linear equation in one or two variables always forms a straight line.

There are two methods to solve such type of problems-

1. Balancing Method

In this method, we have to add or subtract with the same number on both the sides without disturbing the balance to find the solution.

Example

Find the solution for 3x – 10 = 14

Solution

Step 1: We need to add 10 to both the sides so that the numbers and variables come on the different sides without disturbing the balance.

3x – 10 +10 =10+14

3x = 24

Step 2: Now to balance the equation, we need to divide by 3 into both the sides.

3x/3 = 24/3

x = 8

Hence x = 8 is the solution of the equation.

We can recheck our answer by substituting the value of x in the equation.

3x – 10 = 14

3(8) – 10 = 14

24-10 = 14

14 = 14

Here, LHS = RHS, so our solution is correct.

2. Transposing Method

In this method, we need to transpose or transfer the constants or variables from one side to another until we get the solution. When we transpose the terms the sign will get changed.

Example

Find the solution for 2z +10 = 4.

Solution:

Step 1: We transpose 10 from LHS to RHS so that all the constants come in the same side.

2z = 4 -10 (sign will get changed)

2z = -6

Step 2: Now divide both the sides by 2.

2z/2 = – 6/2

z = – 3

Here z = -3 is the solution of the equation.

Some Applications of Linear Equation

We can use the concept of linear equations in our daily routine also. There are some situations where we need to use the variable to find the solution. Like,

• What number should be added to 23 to get 75?

• If the sum of two numbers is 100 and one of the no. is 63 then what will be the other number?

Example

What is the height of the rectangle whose perimeter is 96 cm² and the length is 12 cm?

Solution:

Let the height of the rectangle be ‘s’.

Area of rectangle = Length × Breadth

96 = S × 12

Now, this is a linear equation with variable s.

We need to divide both sides by 12 to find the solution.

96/12 = 12s/12

s = 8

Hence the height of the rectangle is 8 cm.