Number of Sides

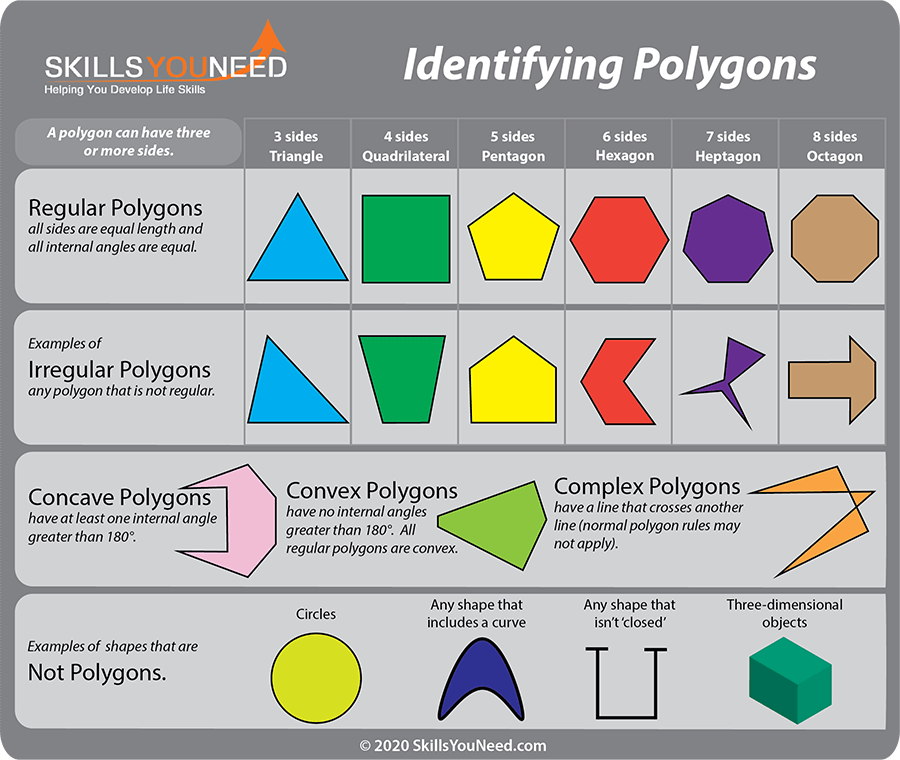
Polygons are usually defined by the number of sides that they have.

Three-Sided Polygons: Triangles

A three-sided polygon is a triangle. There are several different types of triangle (see diagram), including:

• Equilateral – all the sides are equal lengths, and all the internal angles are 60°.
• Isosceles – has two equal sides, with the third one a different length. Two of the internal angles are equal.
• Scalene – all three sides, and all three internal angles, are different.

Triangles can also be described in terms of their internal angles (see our page on Angles for more about naming angles). The internal angles of a triangle always add up to 180°.

A triangle with only acute internal angles is called an acute (or acute-angled) triangle. One with one obtuse angle and two acute angles is called obtuse (obtuse-angled), and one with a right angle is known as right-angled.

Each of these will also be either equilateral, isosceles or scalene.

Four-Sided Polygons – Quadrilaterals

Four-sided polygons are usually referred to as quadrilaterals, quadrangles or sometimes tetragons. In geometry the term quadrilateral is commonly used.

The term quadrangle is often used to describe a rectangular enclosed outdoor space, for example ‘the freshers assembled in the college quadrangle’. The term tetragon is consistent with polygon, pentagon etc. You may come across it occasionally, but it is not commonly used in practice.

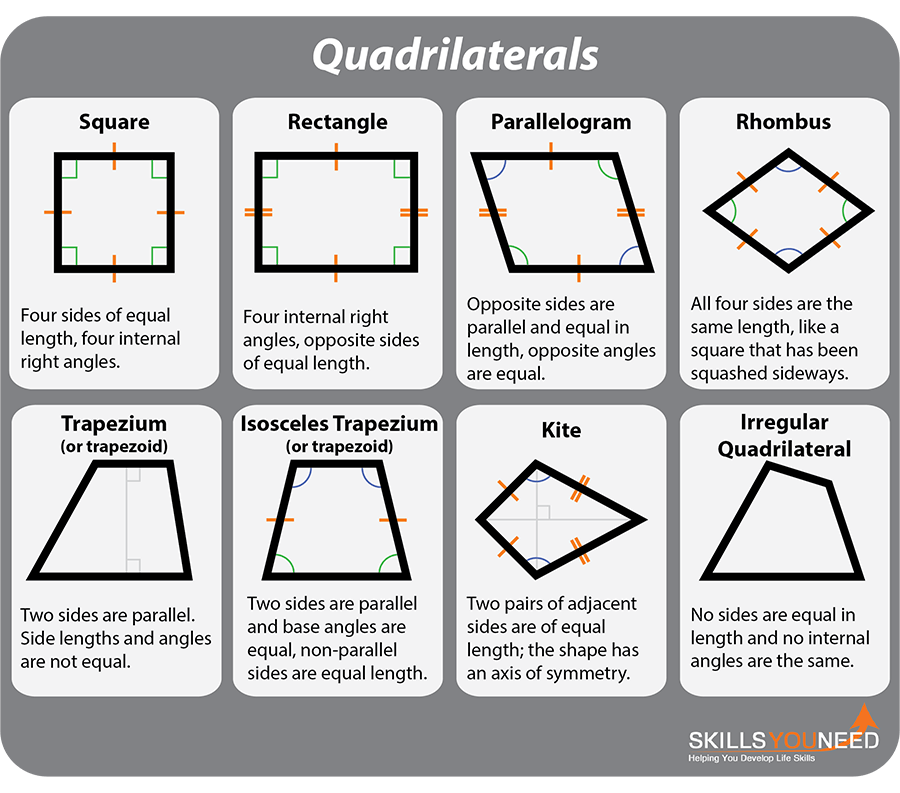
The family of quadrilaterals includes the square, rectangle, rhombus and other parallelograms, trapezium/trapezoid and kite.

The internal angles of all quadrilaterals add up to 360°.

• Square: Four sides of equal length, four internal right angles.

• Rectangle: Four internal right angles, opposite sides of equal length.

• Parallelogram: Opposite sides are parallel, opposite sides are equal in length, opposite angles are equal.

• Rhombus: A special type of parallelogram in which all four sides are the same length, like a square that has been squashed sideways.

• Trapezium (or trapezoid): Two sides are parallel, but the other two sides are not. Side lengths and angles are not equal.

• Isosceles Trapezium (or trapezoid): Two sides are parallel and base angles are equal, meaning that non-parallel sides are also equal in length.

• Kite: Two pairs of adjacent sides are of equal length; the shape has an axis of symmetry.

• Irregular Quadrilateral: a four-sided shape where no sides are equal in length and no internal angles are the same. All internal angles still add up to 360°, as with all other regular quadrilaterals.

More than Four Sides

A five-sided shape is called a pentagon.

A six-sided shape is a hexagon, a seven-sided shape a heptagon, while an octagon has eight sides…

Polygon Names

The names of polygons are derived from the prefixes of ancient Greek numbers. The Greek numerical prefix occurs in many names of everyday objects and concepts. These can sometimes be useful in helping you remember how many sides a polygon has. For example:

• An octopus has eight legs – an octagon has eight sides.
• A decade is ten years – a decagon has ten sides.
• The modern pentathlon has five events – a pentagon has five sides.
• An Olympic heptathlon has seven events – a heptagon has seven sides.

The ‘poly-‘ prefix simply means ‘multiple’, so a polygon is a shape with multiple sides, in the same way that ‘polygamy’ means multiple spouses.

There are names for many different types of polygons, and usually the number of sides is more important than the name of the shape.

There are two main types of polygon – regular and irregular.

A regular polygon has equal length sides with equal angles between each side. Any other polygon is an irregular polygon, which by definition has unequal length sides and unequal angles between sides.

Circles and shapes that include curves are not polygons – a polygon, by definition, is made up of straight lines. See our pages on circles and curved shapes for more.