Course Content
Chapter 01 – Sets
A set is a list of objects in no particular order; they could be numbers, letters, or even words. A Venn diagram is a way of representing sets visually.
0/7
Set Notations
06:41
Operations on Sets
09:44
Let's Try
Venn Diagrams
06:44
Operations on Sets through Venn Diagram
04:45
Let's Try
Math Lab
Chapter 02 – Rational Numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction p/q of two integers, a numerator p, and a non-zero denominator q. In this chapter, we will learn to represent rational numbers on a number line and perform arithmetic operations.
0/5
Rational Numbers
02:29
Rational Number on Number Line
02:04
Operations on Rational Numbers
11:01
Let's Try
Math Lab
Chapter 03 – Decimals
Decimals are a set of numbers lying between integers on a number line. They are just another way to represent fractions in mathematics. In this chapter, we will learn about the conversion of decimals to rational numbers, the kinds of decimals, and absolute values.
0/6
Conversion of Decimals to Rational Numbers
05:18
Terminating and Non-Terminating Decimals
05:40
Stimulation – Area Model Decimals
00:00
Approximate Value
02:28
Dare To Math - Quiz
Math Lab
Chapter 04 – Exponents
The exponent of a number says how many times to use that number in a multiplication. The laws of exponents simplify the multiplication and division operations and help to solve the problems easily. In this chapter, we are going to discuss the six important laws of exponents.
0/4
Base, Exponent and Value
02:07
Laws of Exponent
08:55
Let's Try
Math Lab
Chapter 05 – Square Root of Positive Numbers
Square root, in mathematics, is a factor of a number that, when multiplied by itself, gives the original number. In this chapter, we will learn about what makes perfect squares and will find the roots of positive numbers by considering real-life scenarios.
0/4
Perfect Squares
03:04
Square Root
06:39
Let's Try
Math Lab
Chapter 06 – Direct and Inverse Variation
Variation means change. With direct variation, numbers change proportionately in the same direction, while with inverse variation, they change in opposite directions. In this chapter, we will earn how to solve direct and inverse variation problems, explore their definitions, and work examples to understand the equations and techniques for solving them. Also, we learn to find the continued ratio for two or more ratios.
0/9
Continued Ratio
05:47
Let's Try
Direct Proportion
02:34
Stimulation – Proportion Playground
00:00
Inverse Proportion
05:54
Stimulation – Unit Rates
00:00
Time, Work, and Distance
08:42
Let's Try
Math Lab
Chapter 07 – Financial Arithmetic
Financial mathematics describes the application of mathematics and mathematical modeling to solve financial problems. In this chapter, we will learn about the concept of taxation, profit/markups, zakat & ushr, and how they relate to our daily life.
0/7
Taxes
05:53
Let's Try
Profit and Markup
05:45
Let's Try
Zakat
03:30
Ushr
05:50
Math Lab
Chapter 08 – Algebraic Expressions
Algebraic expressions are the idea of expressing numbers using letters or alphabets without specifying their actual values. The algebraic equations which are valid for all values of variables in them are called algebraic identities. In this chapter, we will learn to perform operations on polynomials and to factorize an algebraic equation by using identities.
0/10
Algebraic Expressions
09:55
Stimulation – Expression Exchange
00:00
Polynomials
08:19
Addition and Subtraction of Polynomials
06:05
Multiplication and Division of Polynomials
05:59
Stimulation – Area Model Algebra
00:00
Algebraic Identities
06:35
Factorization of Algebraic Expressions
07:28
Let's Try
Math Lab
Chapter 09 – Linear Equations
Linear equations are equations having variables with power 1. ax+b = 0 is an example with one variable where x is the variable, and a and b are real numbers. In this chapter, we will learn the definition, type of solutions, and how to solve these equations with one variable and two variables using different methods along with examples.
0/10
Linear Equations
02:15
Solution of Linear Equations
11:20
Stimulation – Equality Explorer
00:00
Let's try
Solving Equation with variables on both sides
07:36
Stimulation – Equality Explorer (Two Variables)
00:00
Solving Fractional Equations
02:23
Simulation – Balancing Equation
00:00
Let's Try
Math Lab
00:00
Chapter 10 – Fundamentals of Geometry
Geometry is the study of different types of shapes, figures, and sizes in Maths or real life. In geometry, we learn about different angles, transformations, and similarities in the figures. It is important to know and understand some basic concepts. We will learn about working in different numbers of dimensions, and about some of the most fundamental concepts in geometry, including points, lines, and planes.
0/7
Properties of an Angle
02:53
Let's Try
Congruent and Similar Figures
03:13
Congruent Triangles
05:59
Circle
03:14
Let's Try
Math Lab
Chapter 11 – Practical Geometry
The practical Geometry chapter will teach you about lines and to construct two-dimensional given different kinds of measurements. A quadrilateral is a closed two-dimensional shape that has four sides and four angles. Any four-sided closed shape such as square, rectangle, rhombus, parallelogram, trapezium, etc. And a closed two-dimensional shape that has 3 sides and 3 angles is known as a triangle.
0/16
Line Segments
02:56
Divide a Line Segment
00:00
Math Lab
Divide a Line Segment in a Given Ratio
00:00
Triangles
01:00
Construction of a Triangle (Perimeters and Ratios Given)
00:00
Construction of an Equilateral Triangle
03:34
Construction of an Isosceles Triangle
00:00
Measures of a Triangle
00:00
Math Lab
Parallelogram
04:34
Construct a Parallelogram (Two Adjacent Sides Given)
00:00
Construction of a Parallelogram (Adjacent Side and Diagonal Given)
00:00
Measures of a Quadrilateral
02:30
Let's Try
Math Lab
Chapter 12 – Circumference, Area and Volume
This topic comes under analytical geometry and the formulas for the volume and the surface area of the sphere were first discovered by Archimedes. In this chapter, we will learn about the area and volume of two-dimensional and three-dimensional shapes.
0/6
Circumference and Area of a Circle
07:03
Simulation – Surface Area
00:00
Surface Area of a Cylinder
03:08
Volume of a Cylinder
03:51
Dare To Math - Quiz
Math Lab
Chapter 13 – Information Handling
Frequency distribution, in statistics, is a graph or data set organized to show the frequency of occurrence of each possible outcome of a repeatable event observed many times. And, a pie chart is a way of representing data in a circular graph. Pie slices of the chart show the relative size of the data. In this chapter, we will learn to construct the frequency distribution table, some new pie chart vocabulary, and learn to construct the pie chart to represent the data.
0/5
Frequency Distribution
03:13
Bar Graphs
02:28
Pie Chart
12:23
Let's Try
Math Lab
Grade 7 – Mathematics
About Lesson

Surface Area of Cylinder

The surface area of a cylinder can be defined as the total space covered by the flat surfaces of the bases of the cylinder and its curved surface. The total surface area of the cylinder has two components – a curved surface area and two flat surface areas.

 

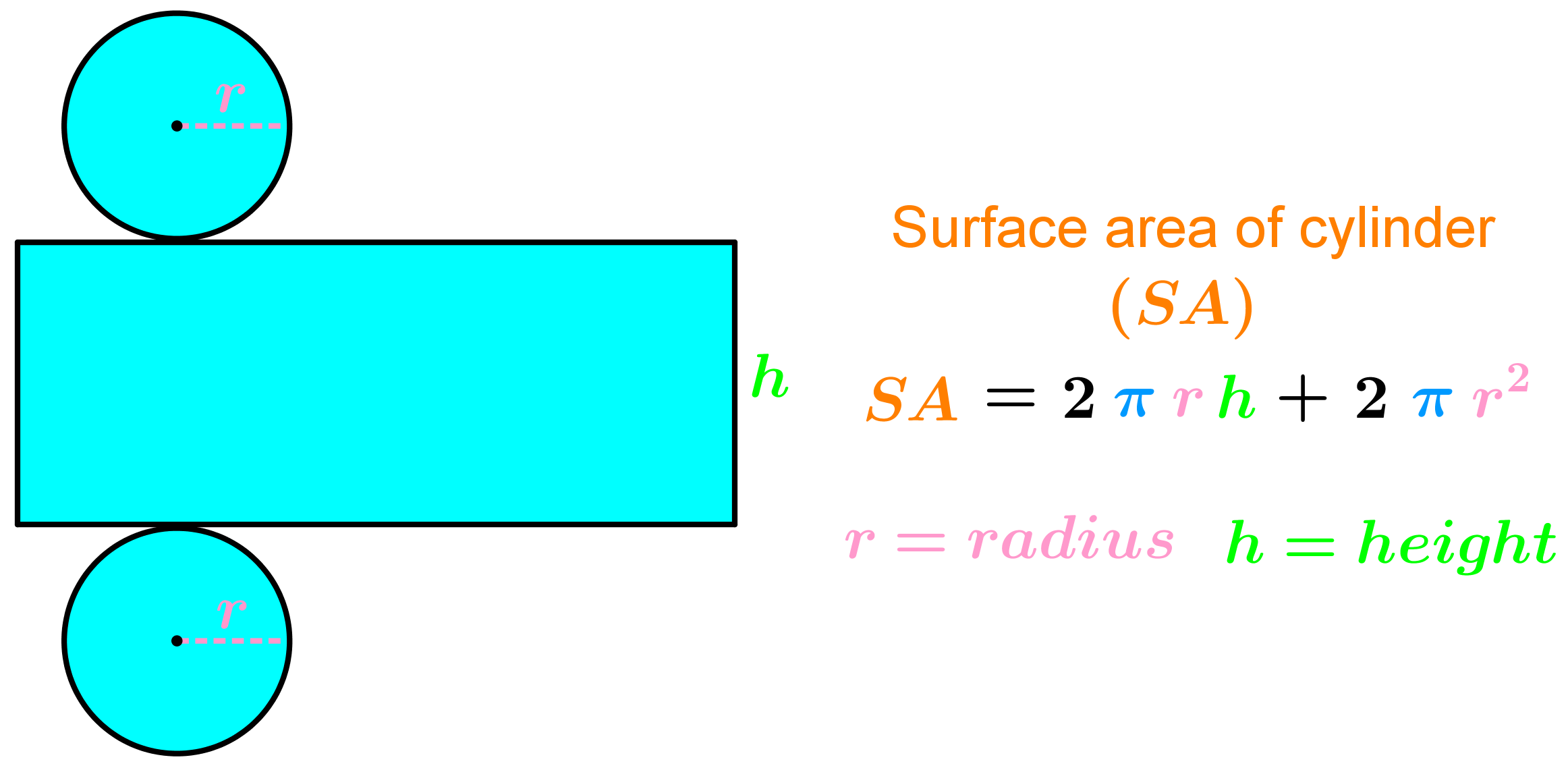
cylinder surface area formula

 

Formula of Surface Area of a Cylinder

The formula for the surface area of the cylinder is used to find the surface area occupied by the bases of the cylinder and the curved surface of the cylinder. Since a cylinder has a curved surface, we can express its curved surface area as well as total surface area. This means that a cylinder has two kinds of surface areas -Total Surface Area (TSA) and Curved Surface Area (TSA).

 

Curved Surface Area of Cylinder

The curved surface area of a cylinder is the surface area covered by its curved surface only. If the radius of the base of the cylinder is ‘r’ and the height of the cylinder is ‘h’, the curved surface area of a cylinder is calculated using the following formula:

 

Curved Surface Area of Cylinder Formula

Curved surface area of cylinder = 2πrh

where,

  • r = radius of the cylinder
  • h = height of cylinder
  • π = 22/7 or 3.14

 

Example: Find the Curved surface area of a cylinder of radius 7 cm and height 14 cm.

Solution: 

The curved surface area of a cylinder can be calculated using the formula, CSA = 2πrh.

After substituting the value of r = 7, h = 14, we get:

CSA = 2πrh

         = 2 × 3.14 × 7 × 14

         = 615.8 cm2

 

Total Surface Area of Cylinder

The total surface area of the cylinder is obtained by adding the area of the two bases and the area of the curved surface. Thus, the formula for the total surface area of the cylinder is given as,

Total surface area of cylinder = Area of two bases + Area of the curved surface. Since the bases of the cylinder are circular in shape, their combined area will be πr2 + πr2. We already know that the curved surface area of a cylinder is 2πrh.

Total surface area of cylinder ⇒ (πr2 + πr2) + 2πrh

⇒ 2πr2 + 2πrh

Total surface area of cylinder = 2πr(r+h)

where,

  • r = radius of the cylinder
  • h = height of cylinder

 

Example: Find the Total surface area (TSA) of a cylinder of radius 5 cm and height 8 cm.

Solution: 

The Total surface area (TSA) of a cylinder can be calculated using the formula, TSA = 2πr(r + h).

After substituting the value of r = 5, h = 8, we get:

TSA = 2πr(r + h)

         = 2 × 3.14 × 5(5 + 8)

         = 615.8 cm2

Exercise Files
surface-area-of-cylinders-worksheet.pdf
Size: 11.73 KB
Previous
Next
0% Complete